复合函数的求导法则
复合函数的求导法则
函数四则运算的求导法则解决了由可导函数的四则运算所构成的函数的求导问题. 复合函数的求导法则可以解决由可导函数所构成的复合函数的求导问题,从而使可以求导的函数的范围得到极大扩充. 这样,一般初等函数的求导问题便可以得到完善的解决.
本书不加证明地给出复合函数的求导法则,需要了解其证明的读者可以查阅《高等数学》(同济大学数学教研室主编,高等教育出版社)等相关参考书.
定理(复合函数求导法则)设函数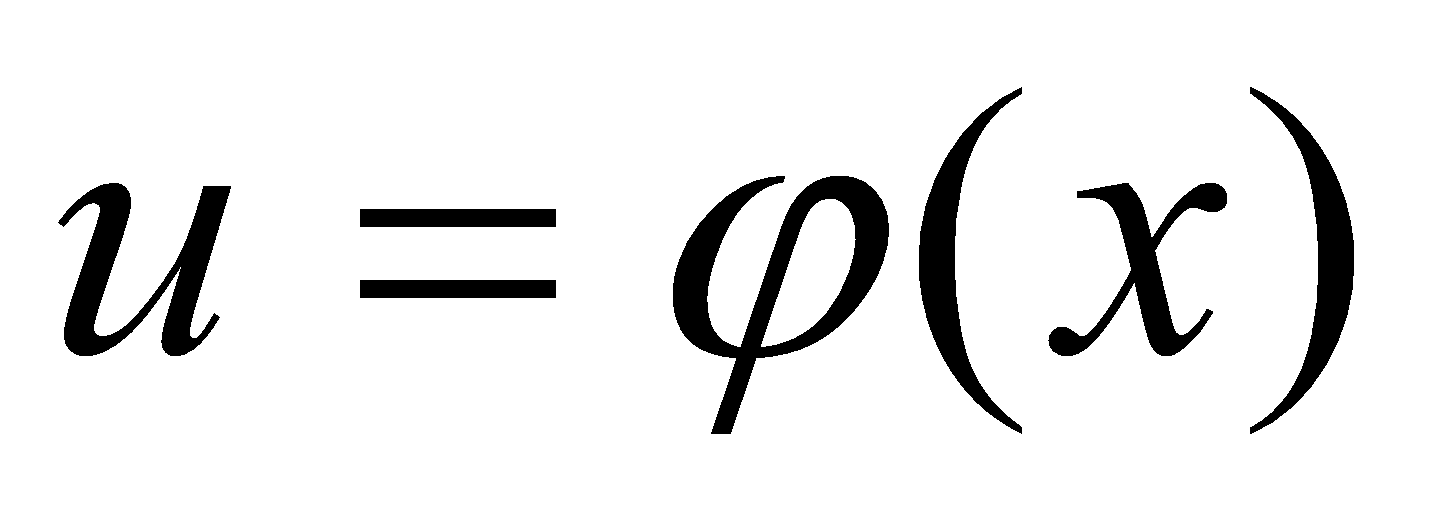 在点
在点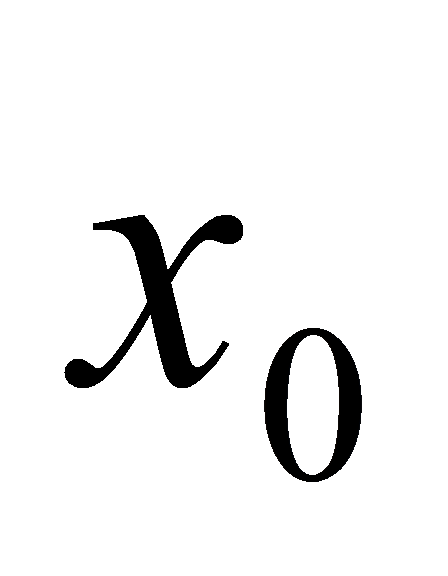 处可导,
处可导,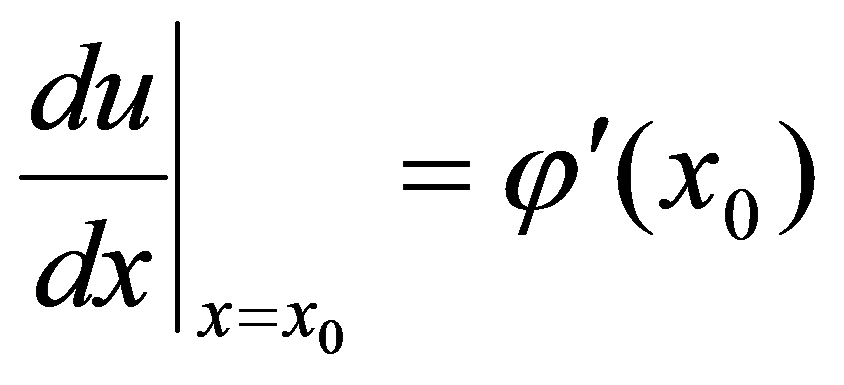 ,函数
,函数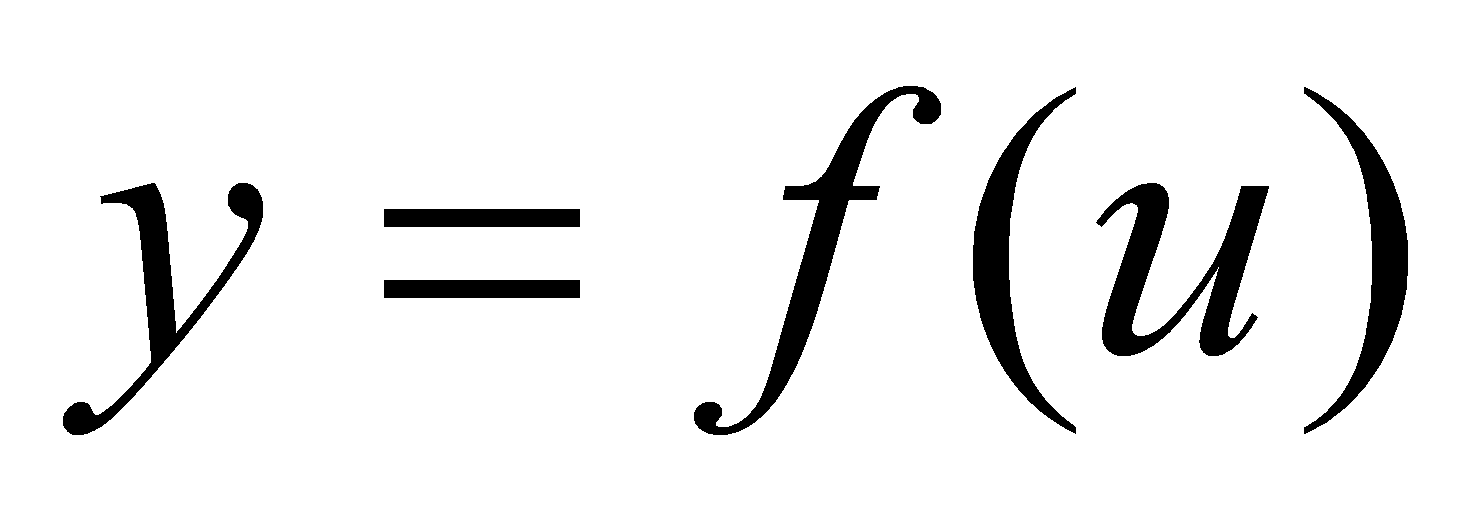 在相应的点
在相应的点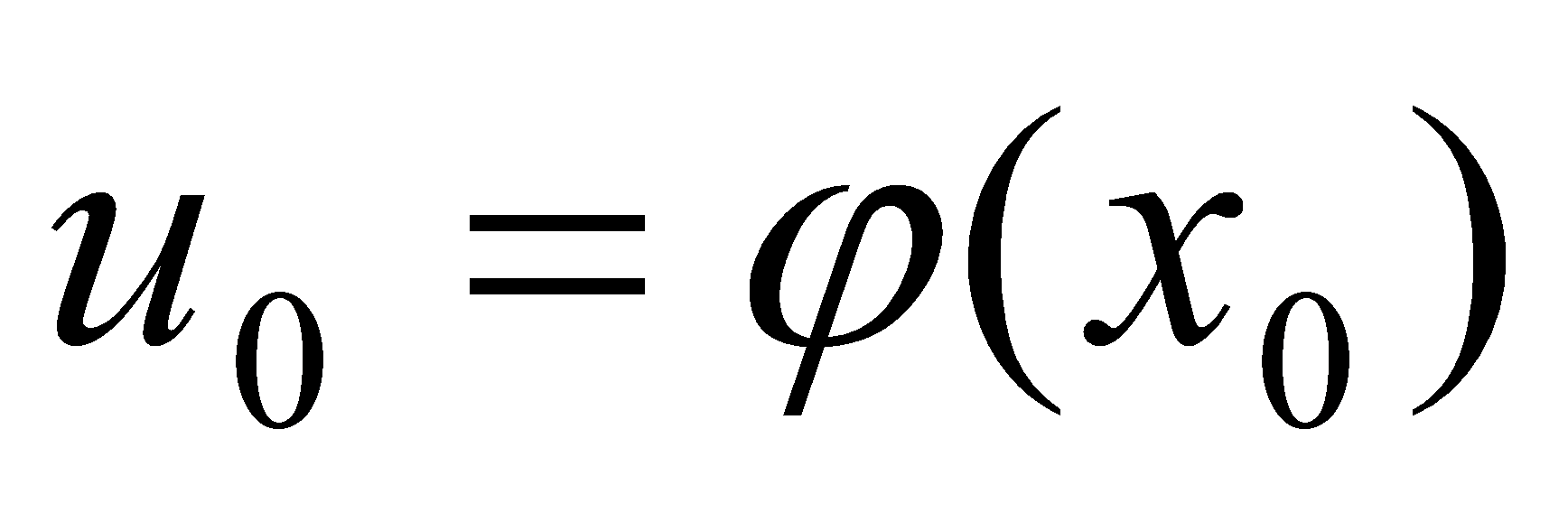 处可导,
处可导,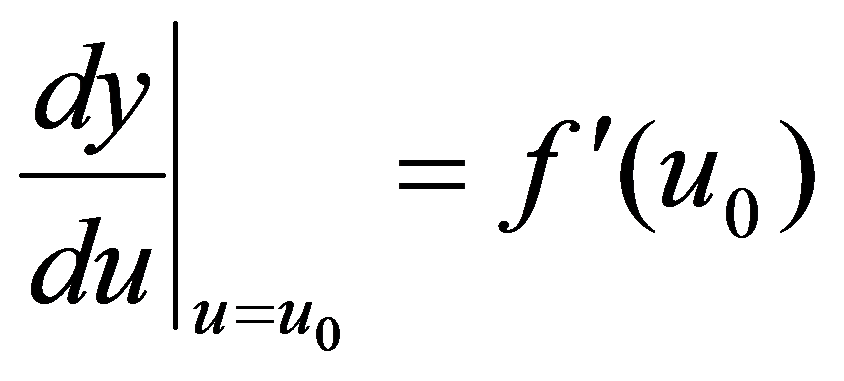 ,则复合函数
,则复合函数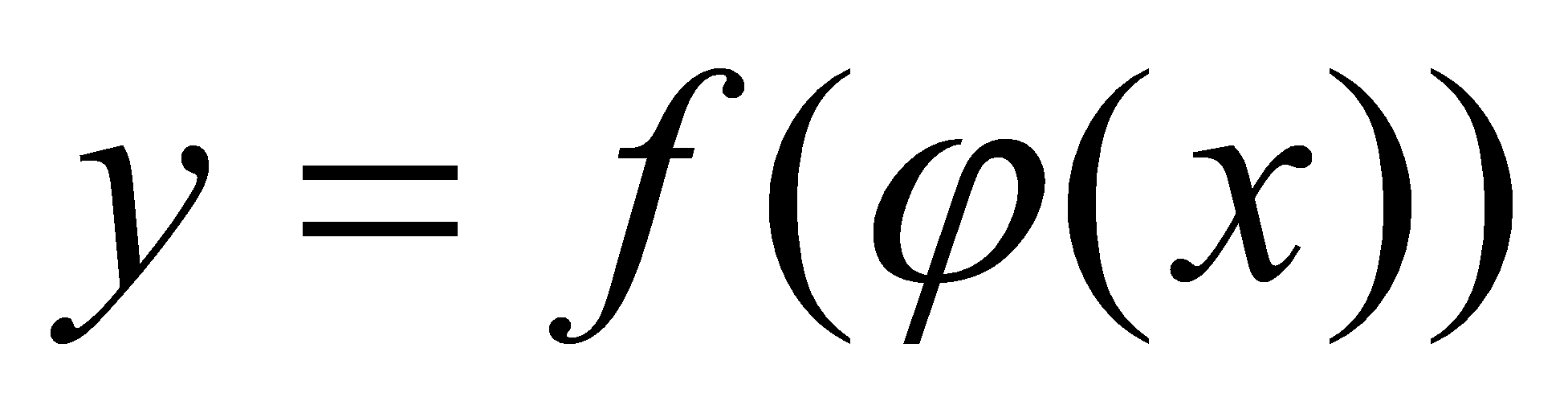 在点
在点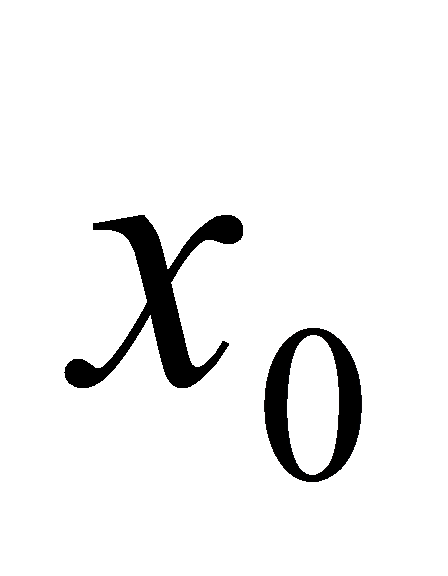 处可导,且其导数为
处可导,且其导数为
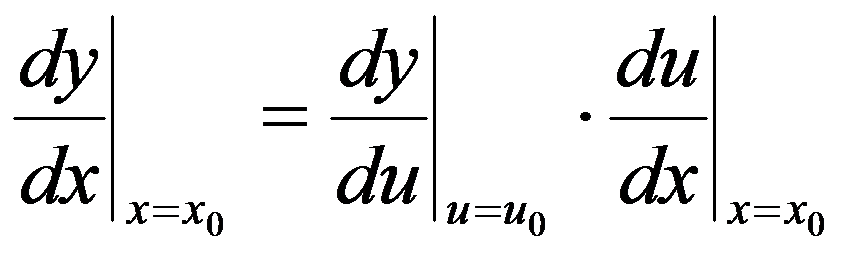 .
.
根据复合函数求导法则,如果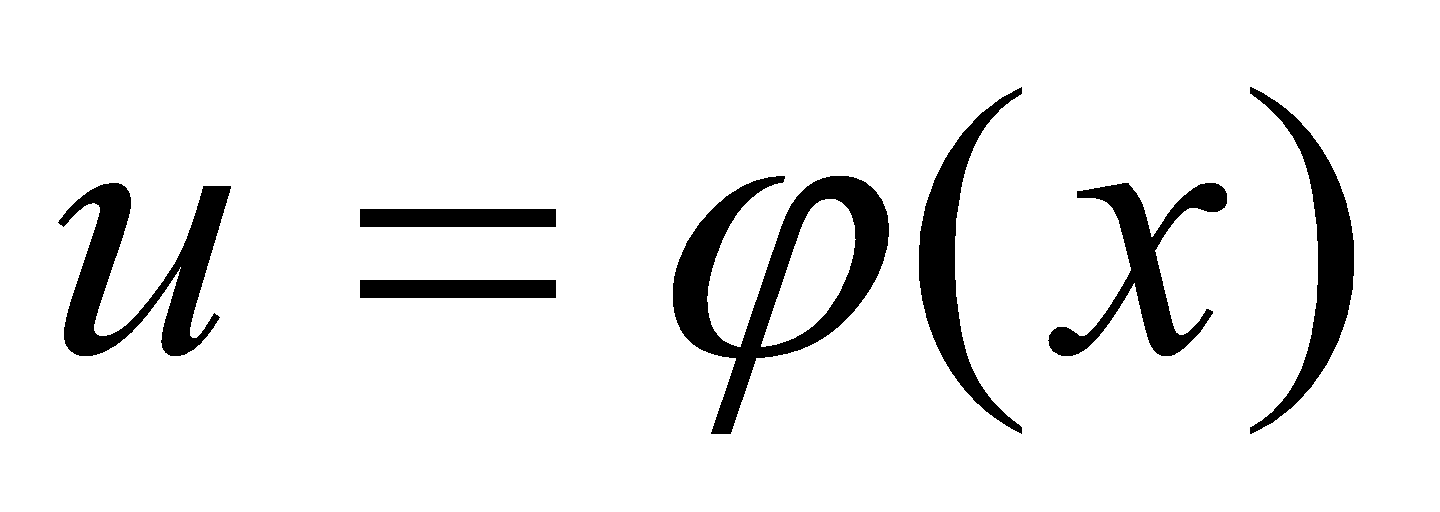 在开区间
在开区间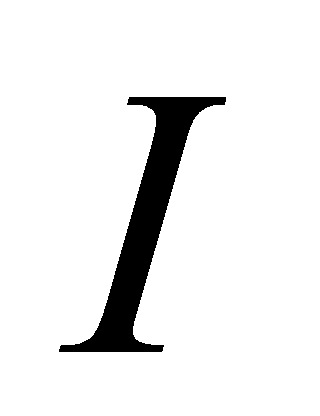 内可导,
内可导,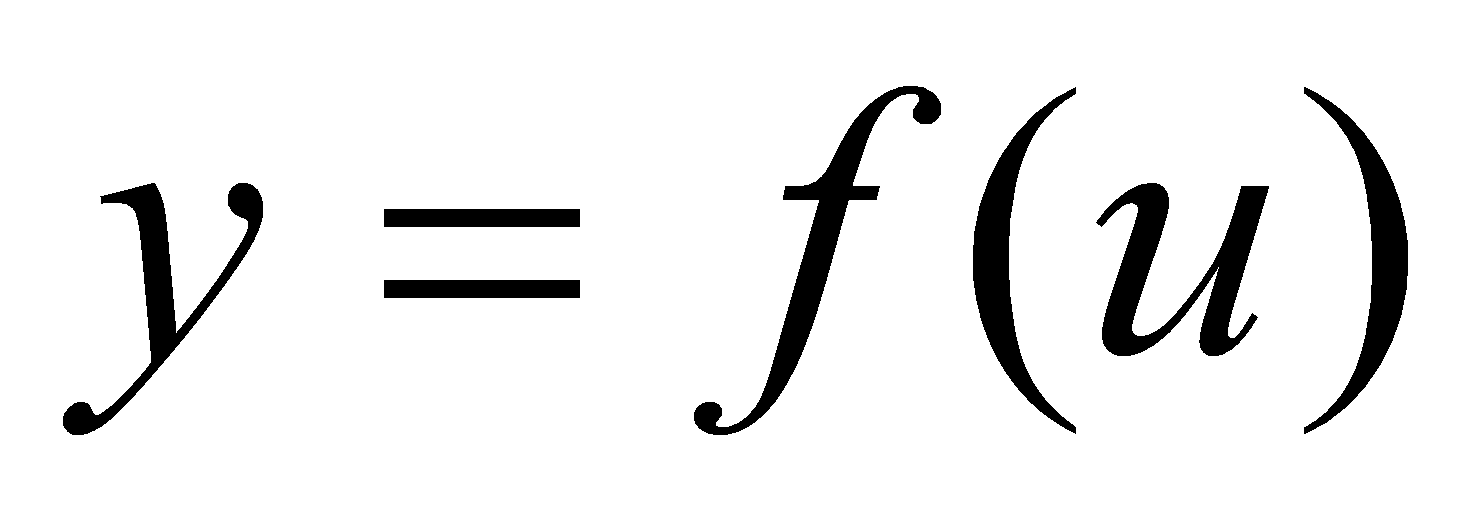 在开区间
在开区间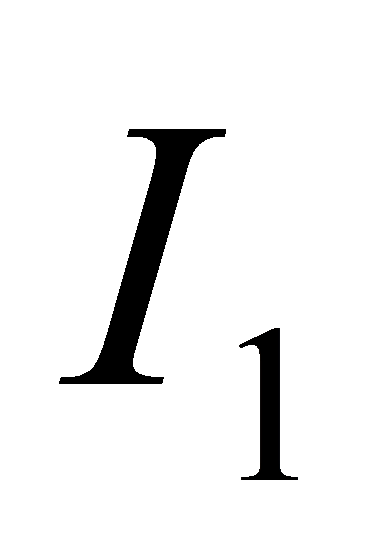 内可导,且当
内可导,且当 时,相应的
时,相应的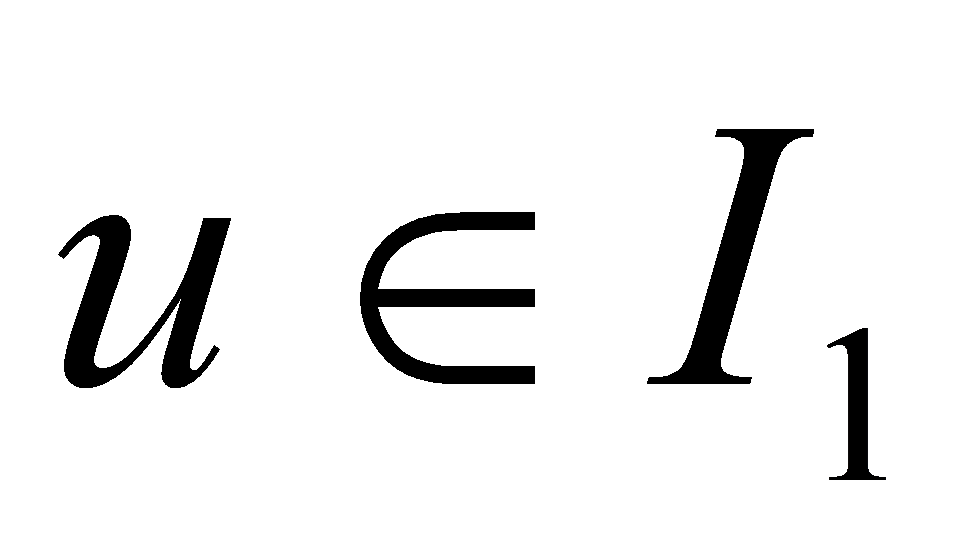 ,则复合函数
,则复合函数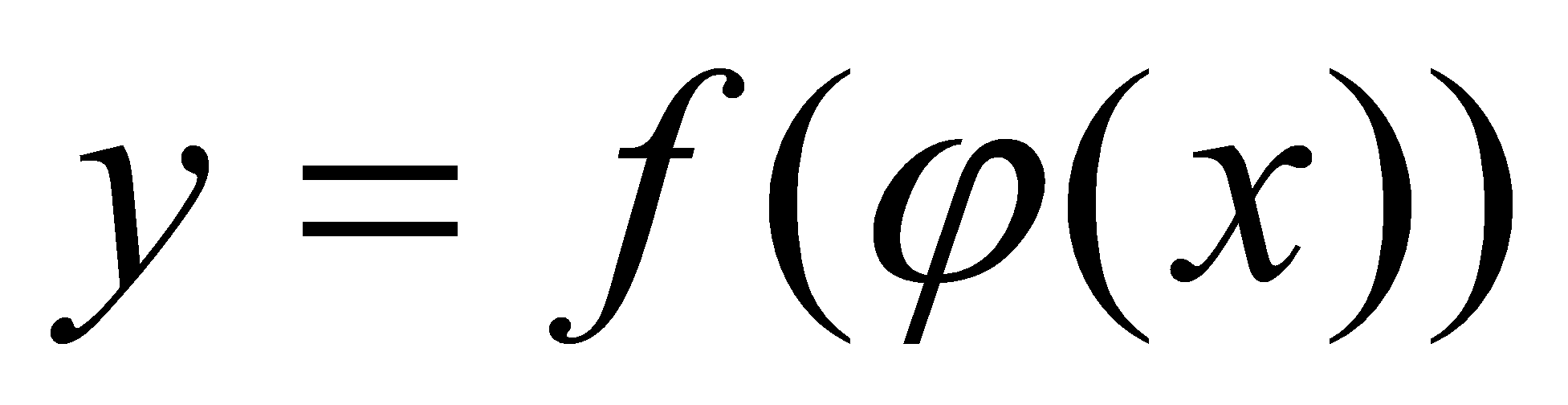 在开区间
在开区间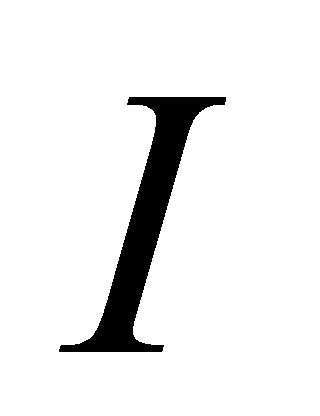 内可导,且
内可导,且
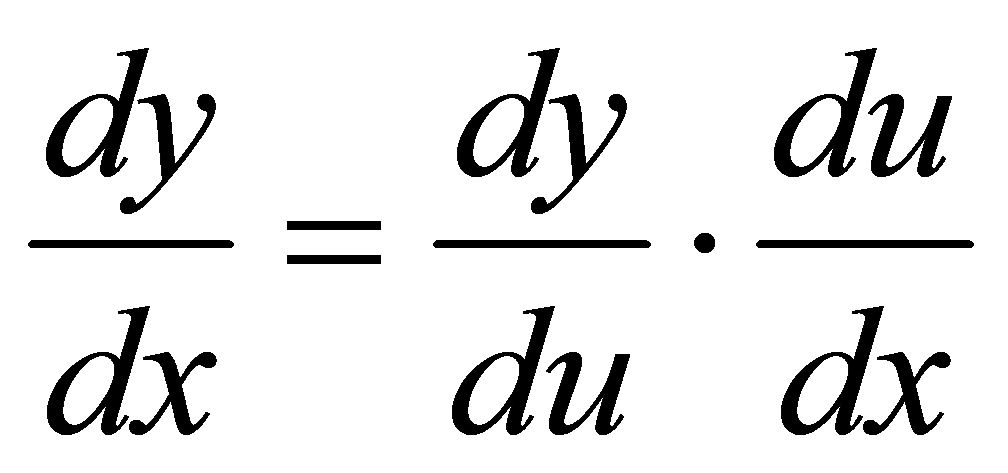 . ()
. ()
()式也可表示为 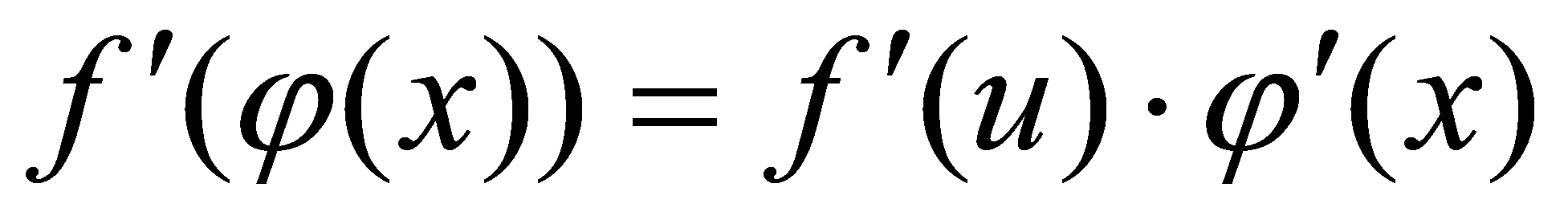 ,
,
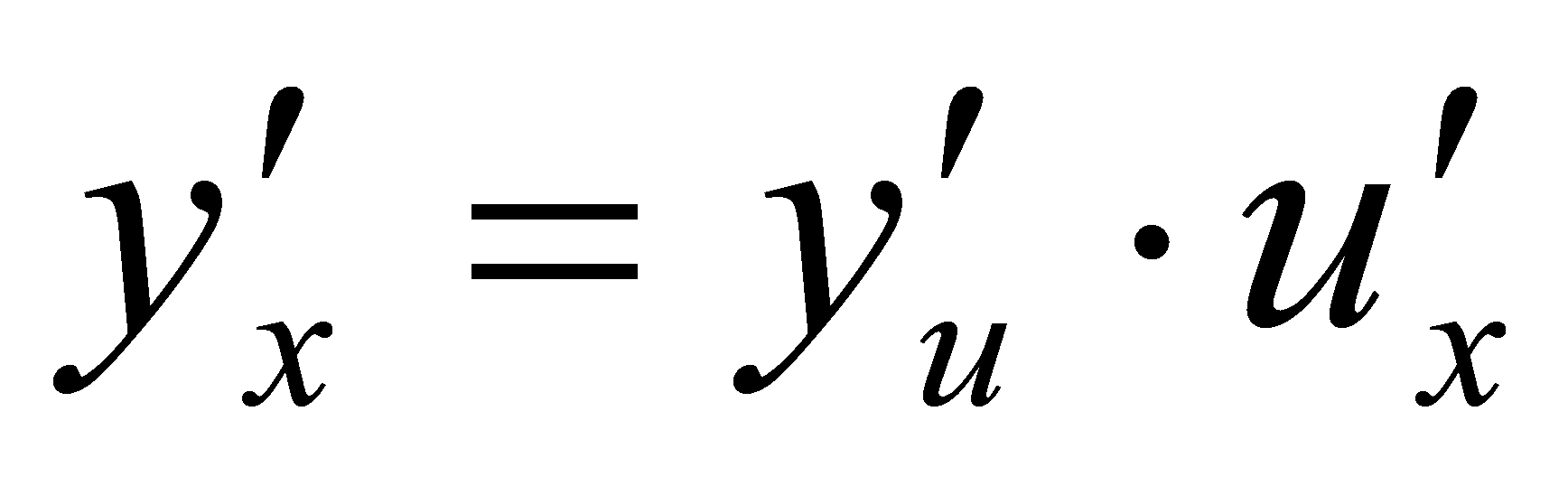 .
.
例求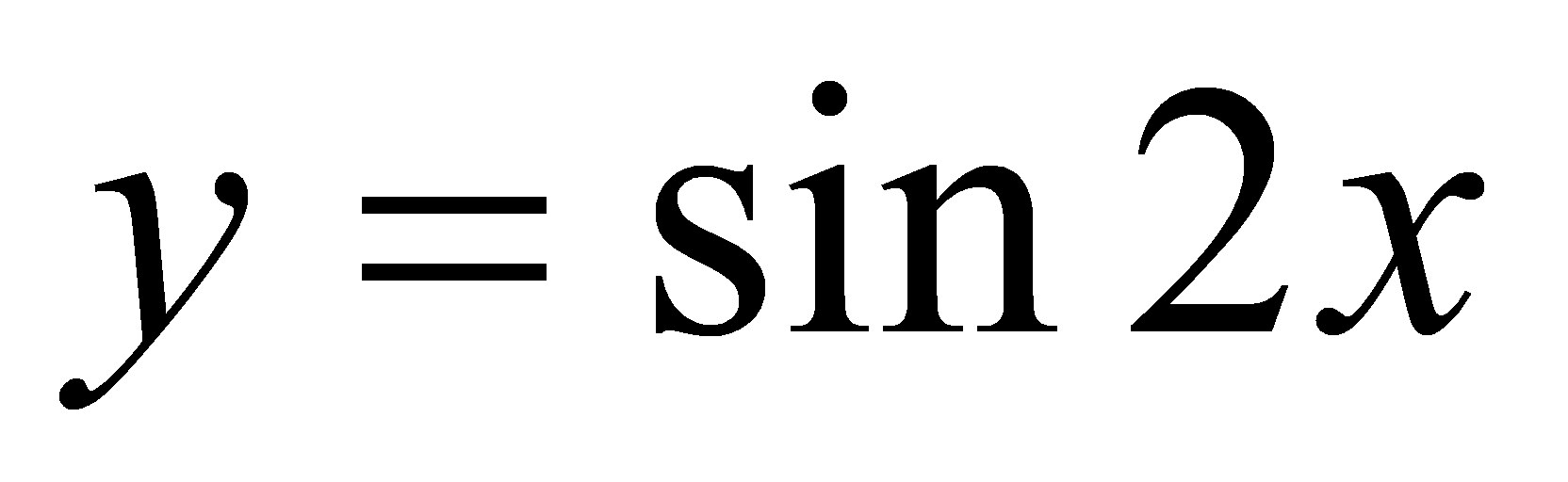 的导数.
的导数.
解令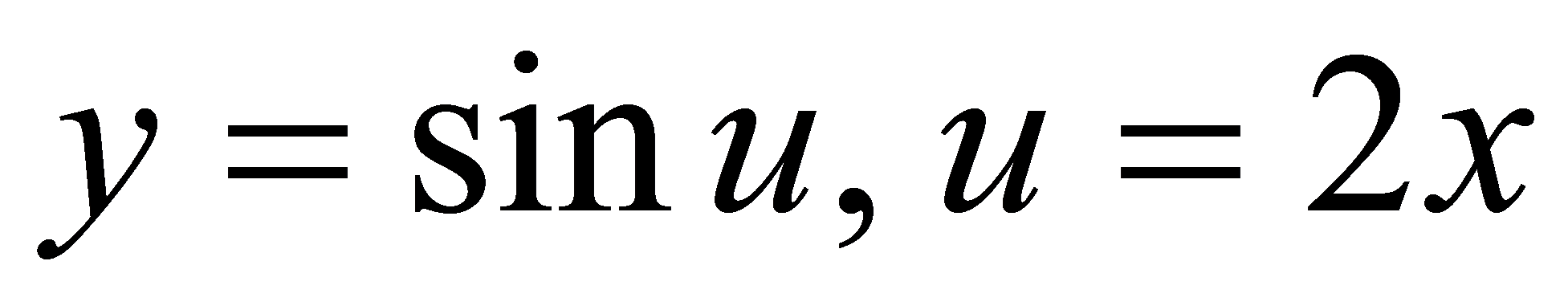 ,
,
则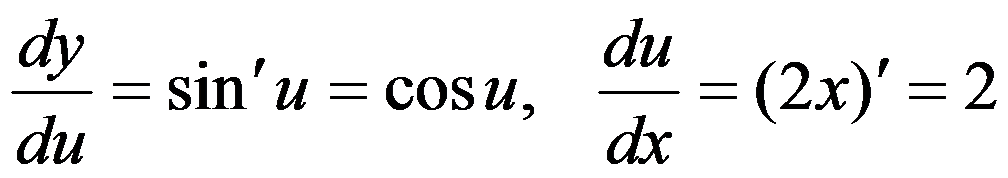 ,
,
根据定理,有: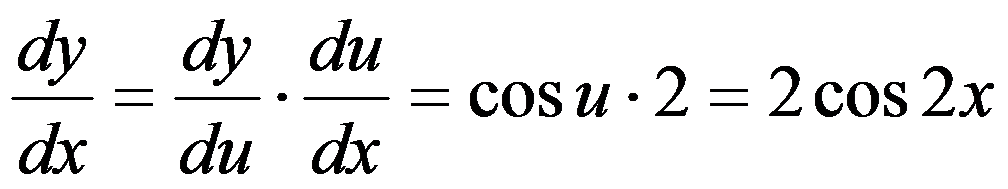 .
.
例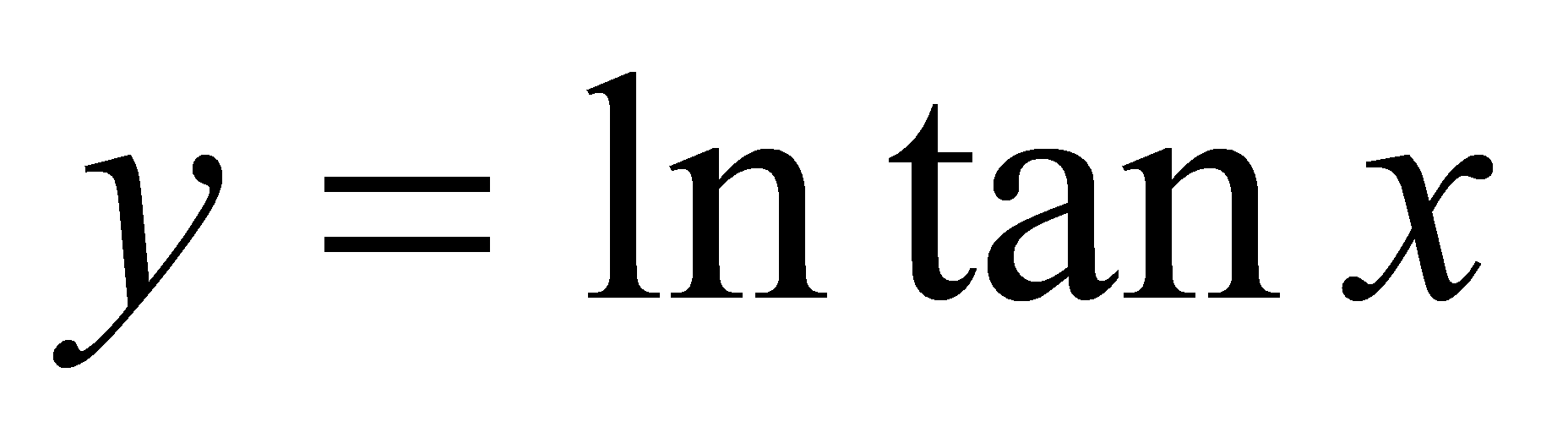 ,求
,求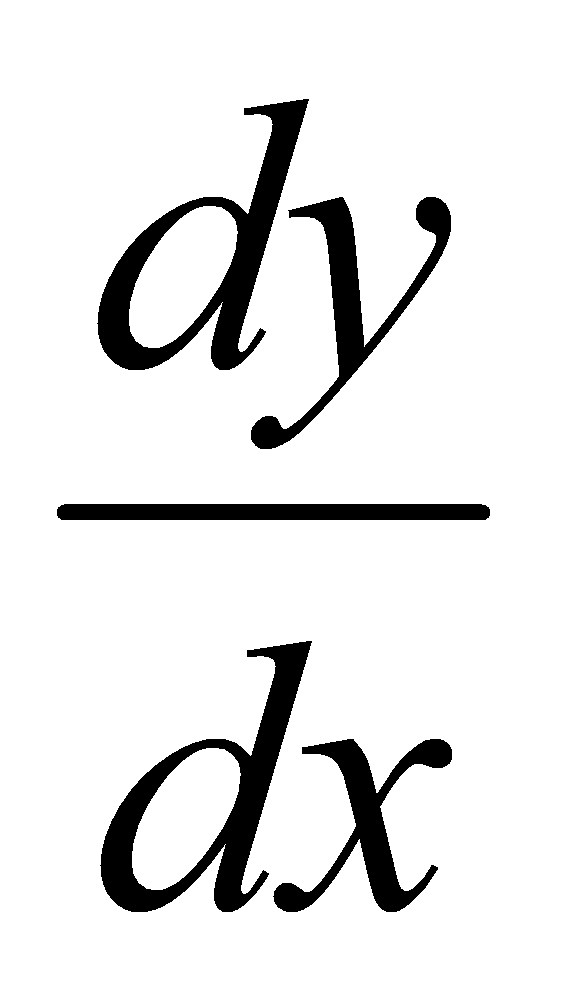 .
.
解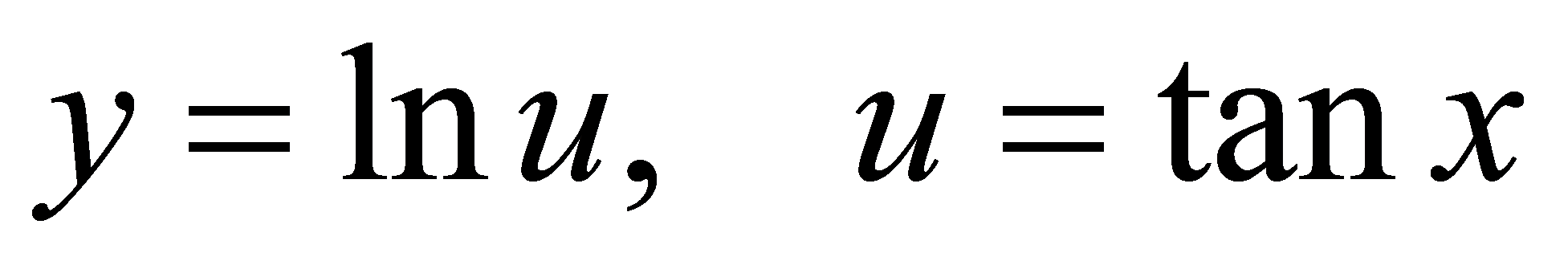 ,
,
则 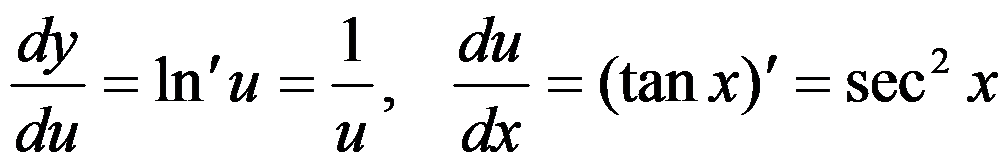 ,
,
由定理,有: 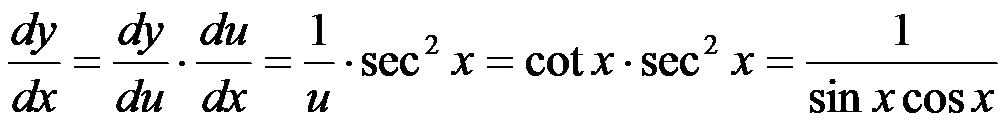 .
.
利用复合函数求导法则可以证明一般的幂函数的导数()式.
例证明幂函数导数公式: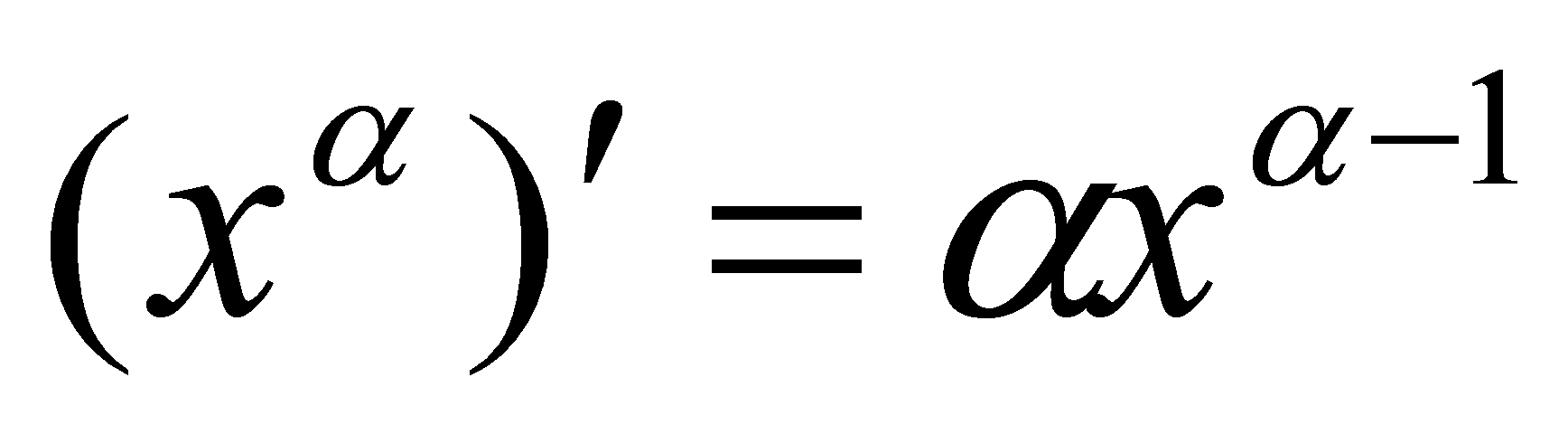 (
( 为任意常数).
为任意常数).
证明设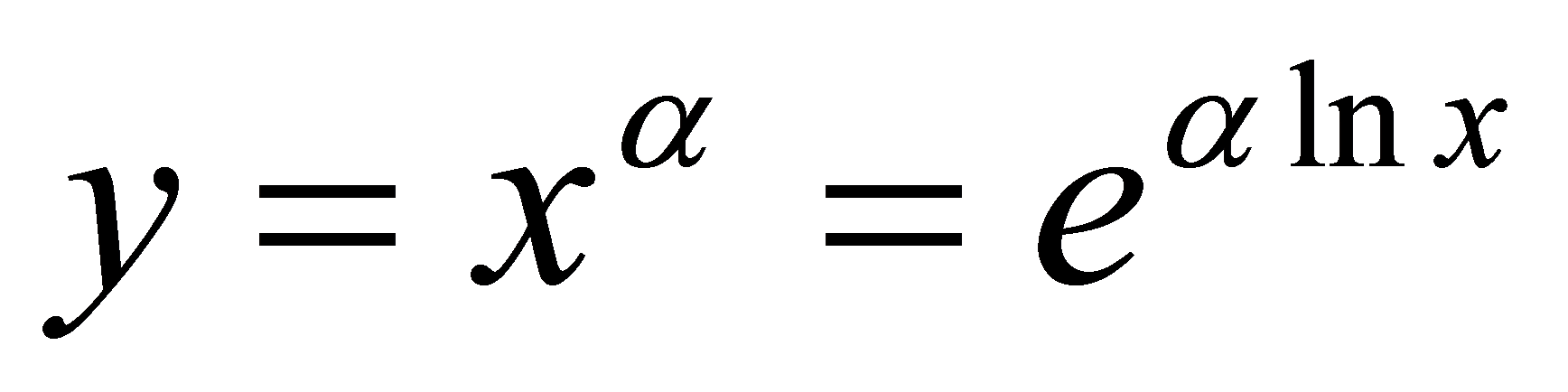 , 令
, 令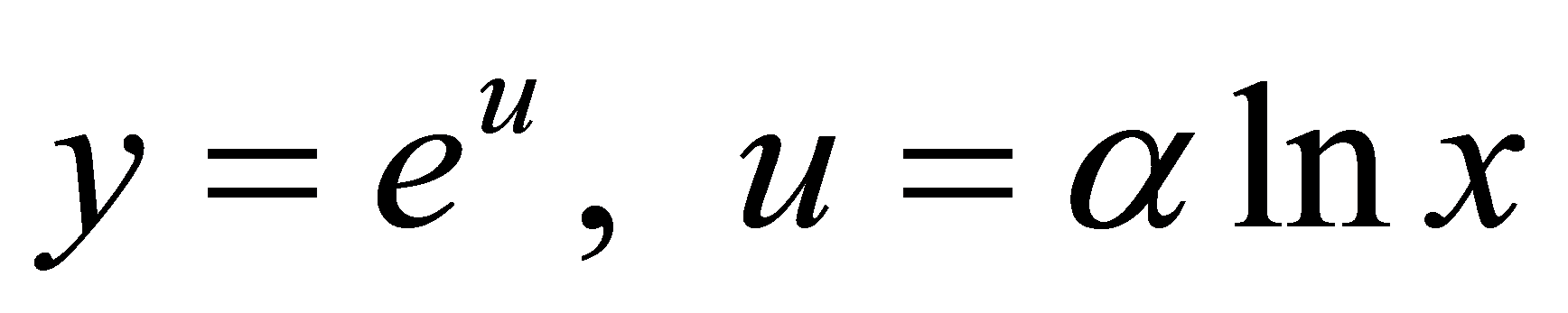 ,
,
则 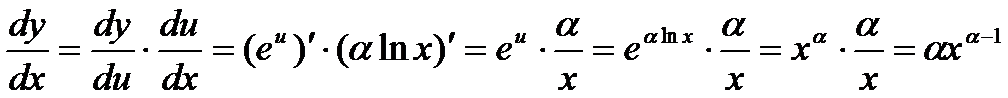 ,
,
即 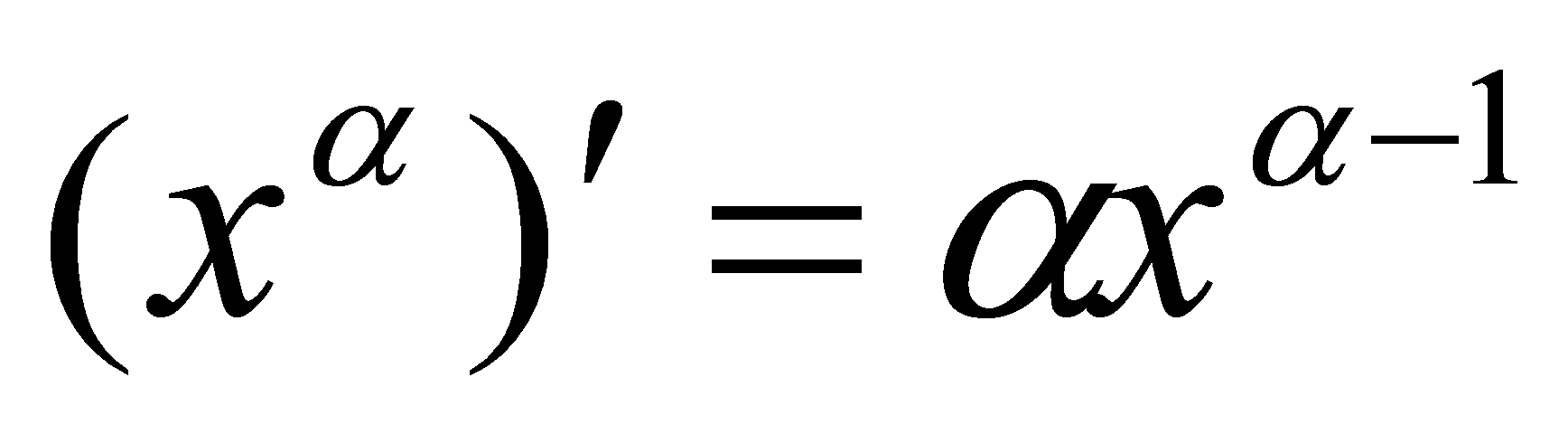 .
.
复合函数求导过程熟悉后,可不必写出中间变量,直接按照法则写出求导过程. 示例如下.
例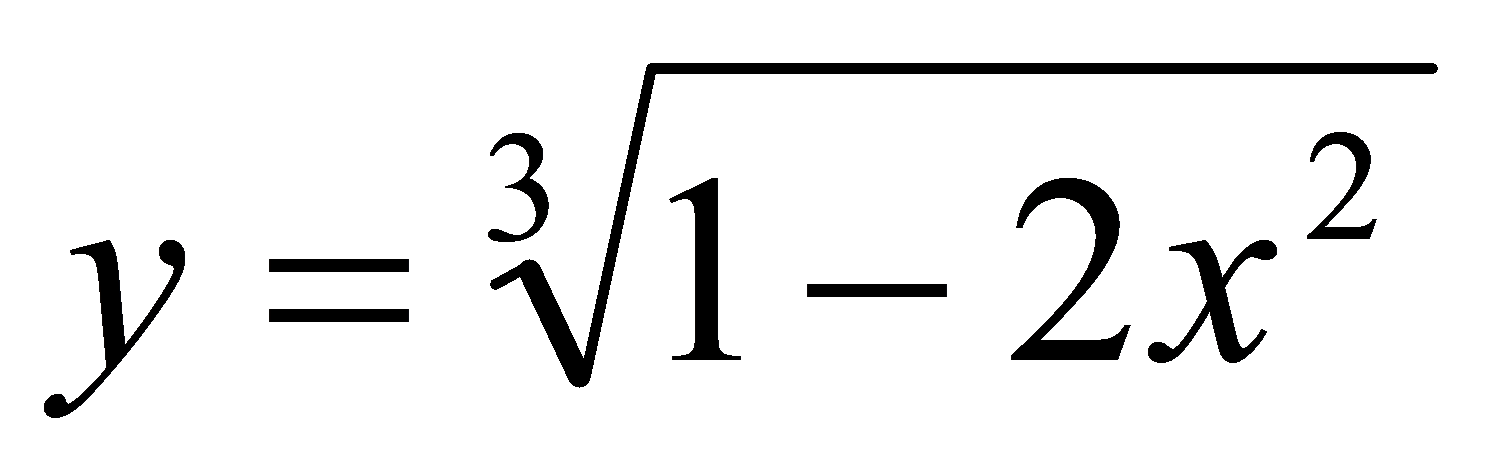 ,求
,求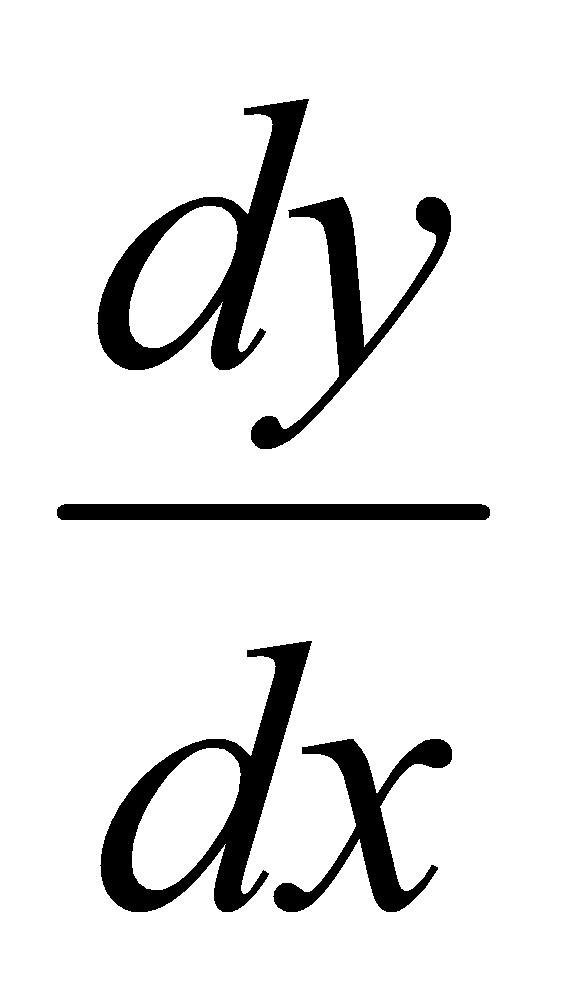 .
.
解
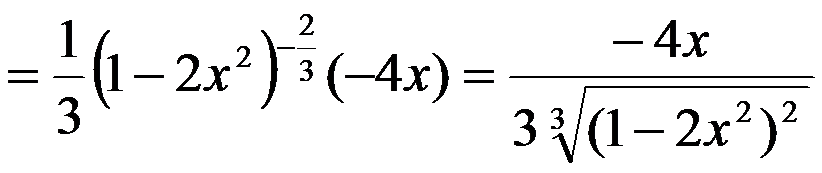 .
.
复合函数的求导法则可以推广到经多个中间变量多重复合的情形.以两个中间变量为例加以说明.
设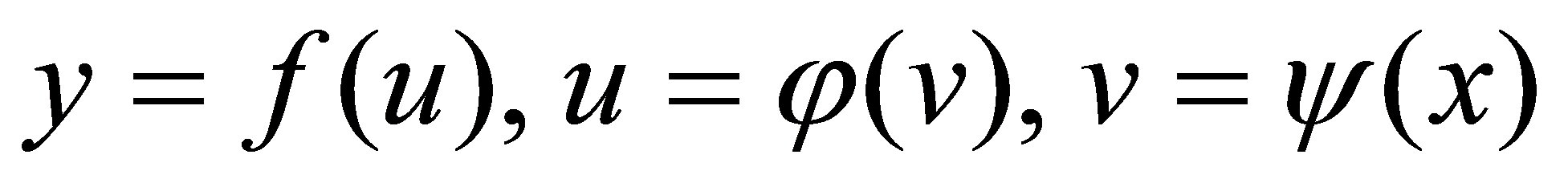 均为可导函数,则
均为可导函数,则
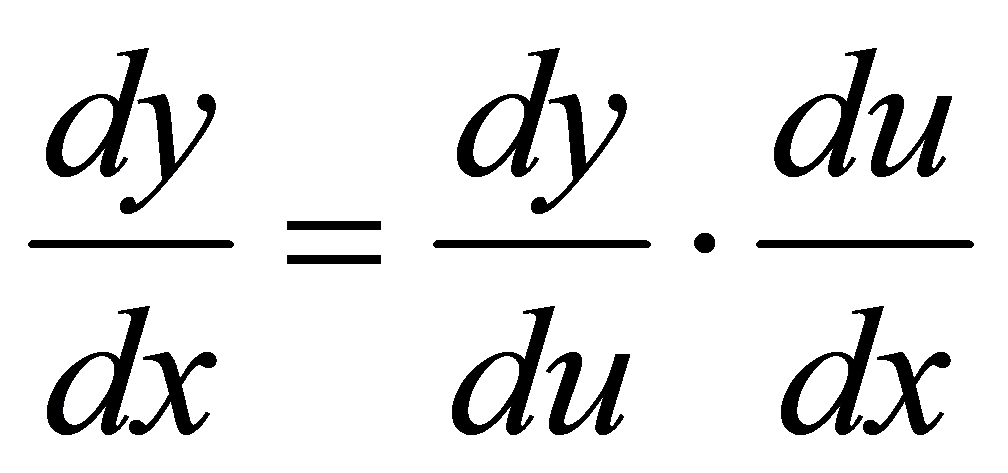 ,()
,()
而 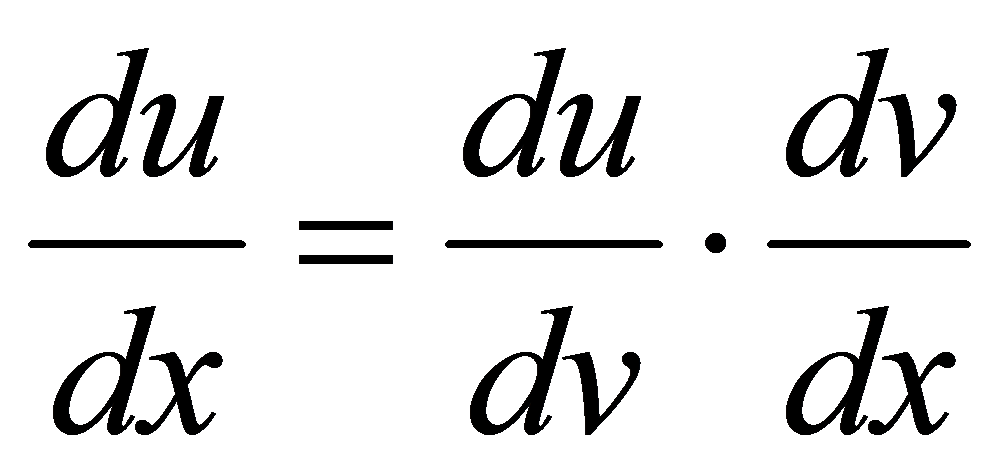 , ()
, ()
将()代入(2.3.2),可知复合函数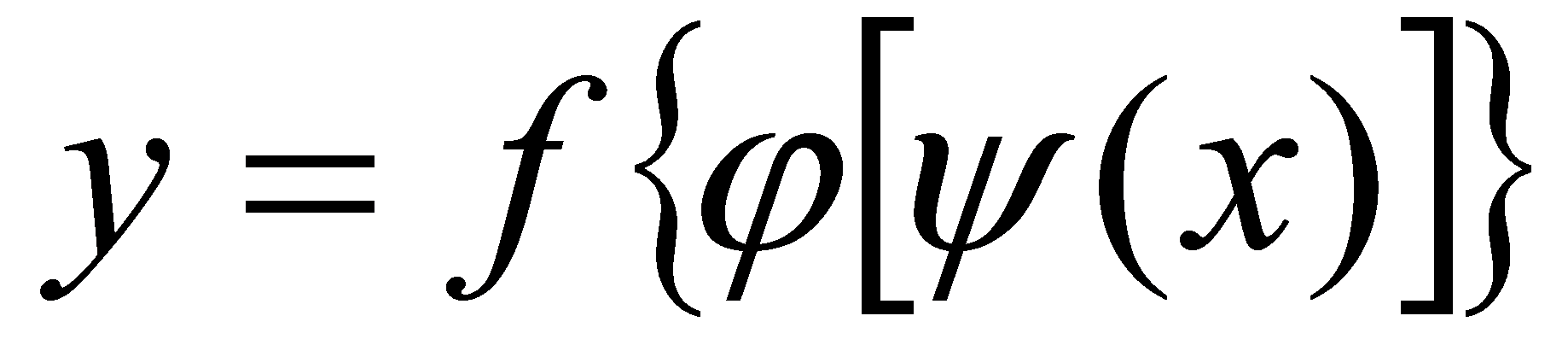 的导数为
的导数为
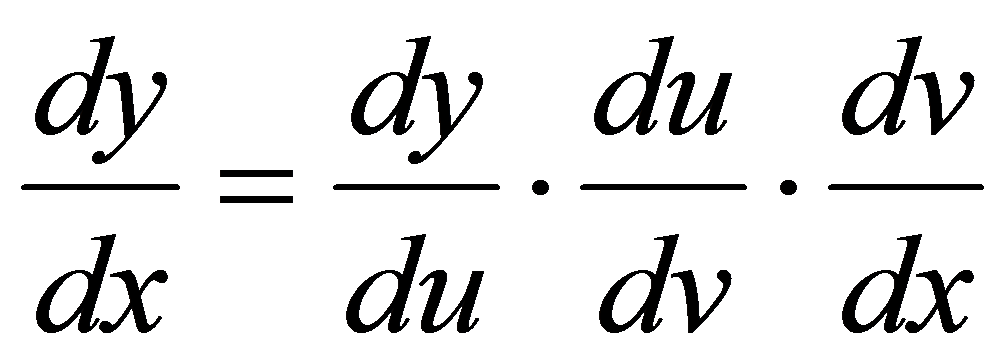 . ()
. ()
例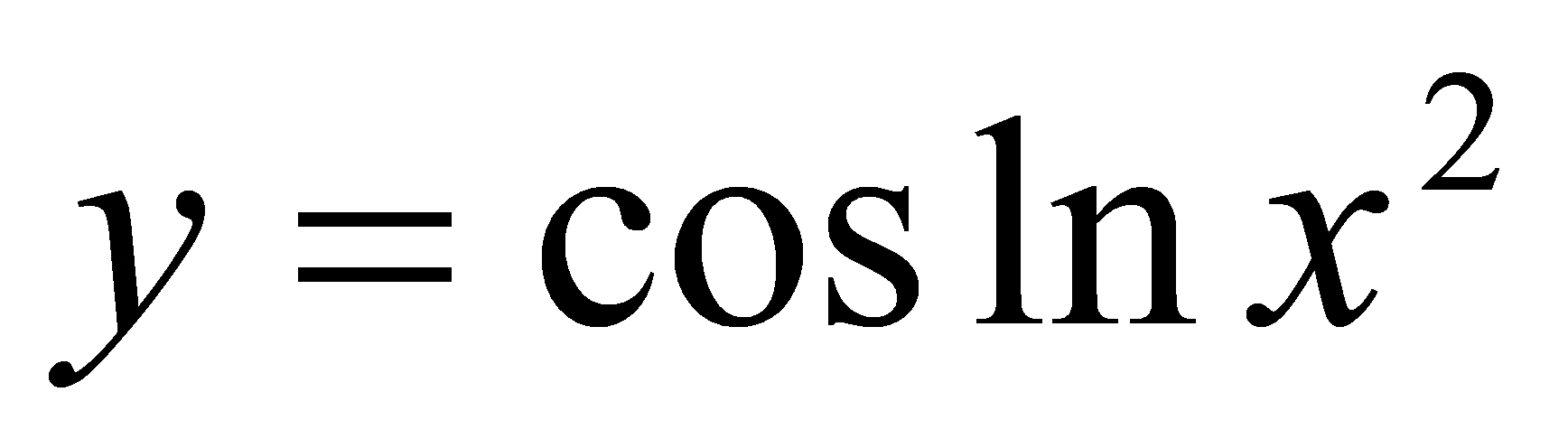 ,求
,求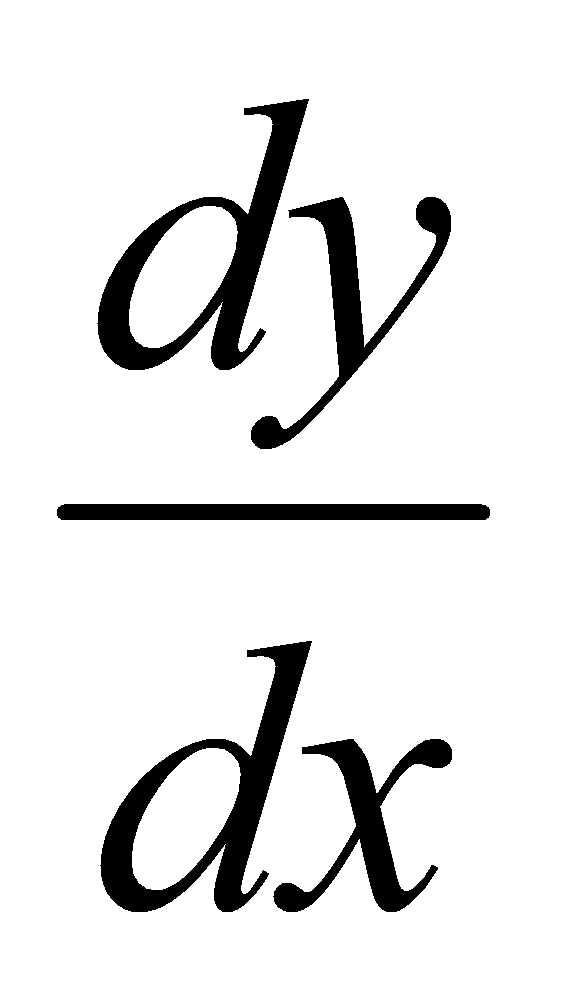 .
.
解函数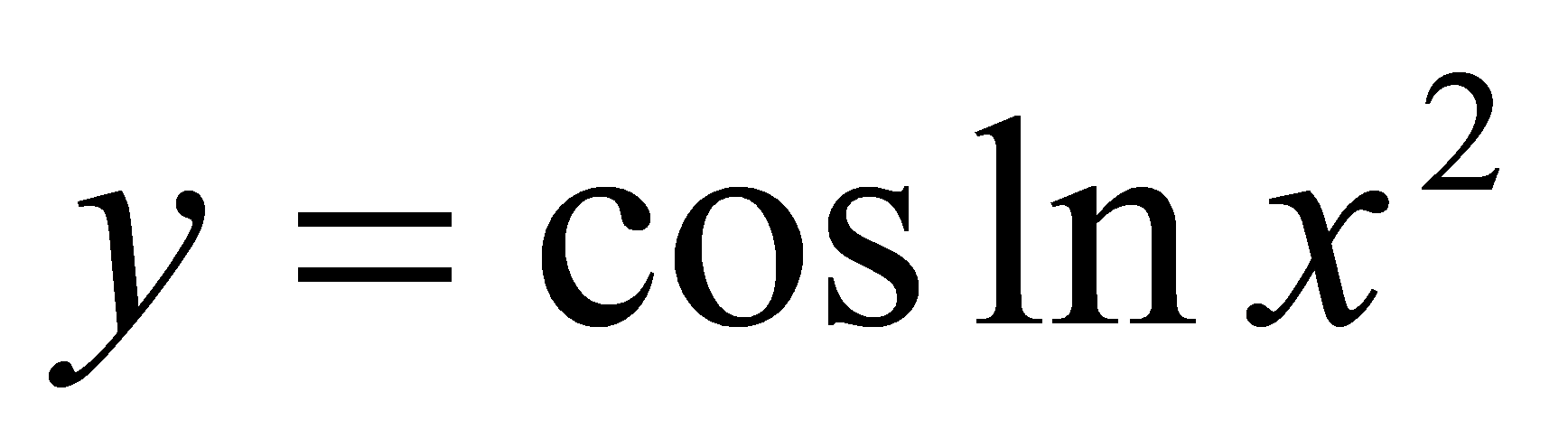 可分解为
可分解为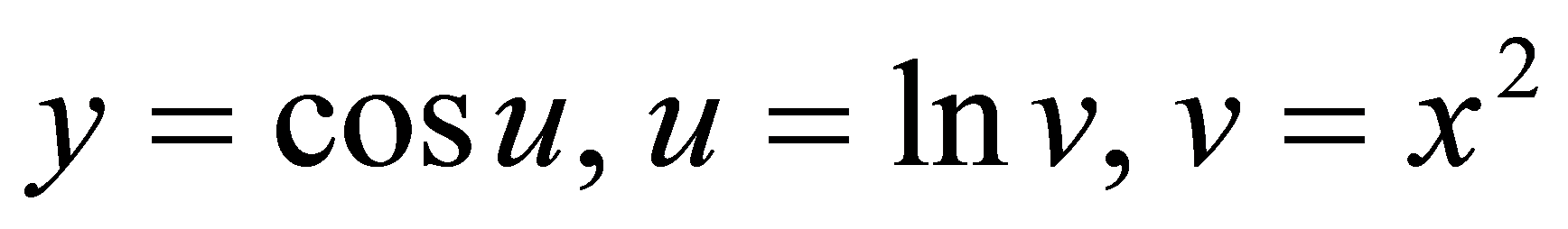 .因
.因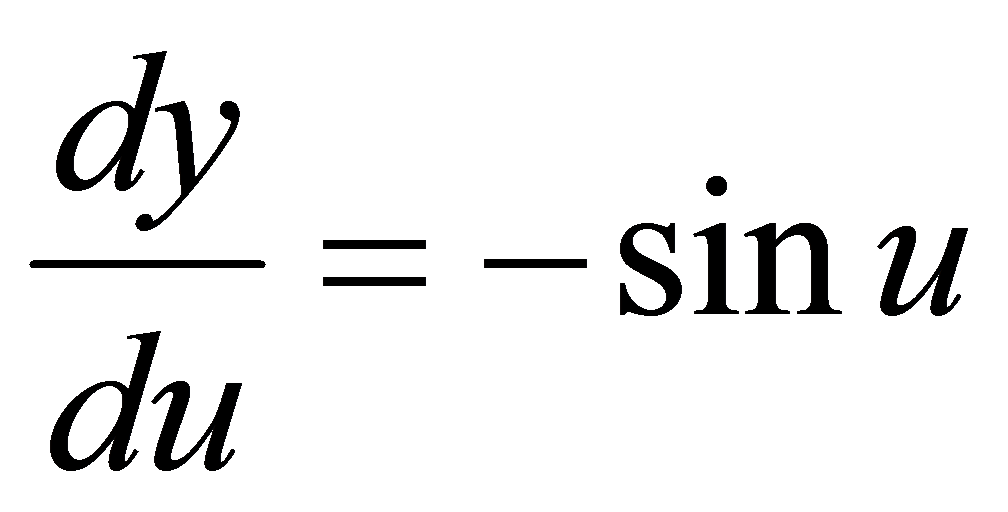 ,
,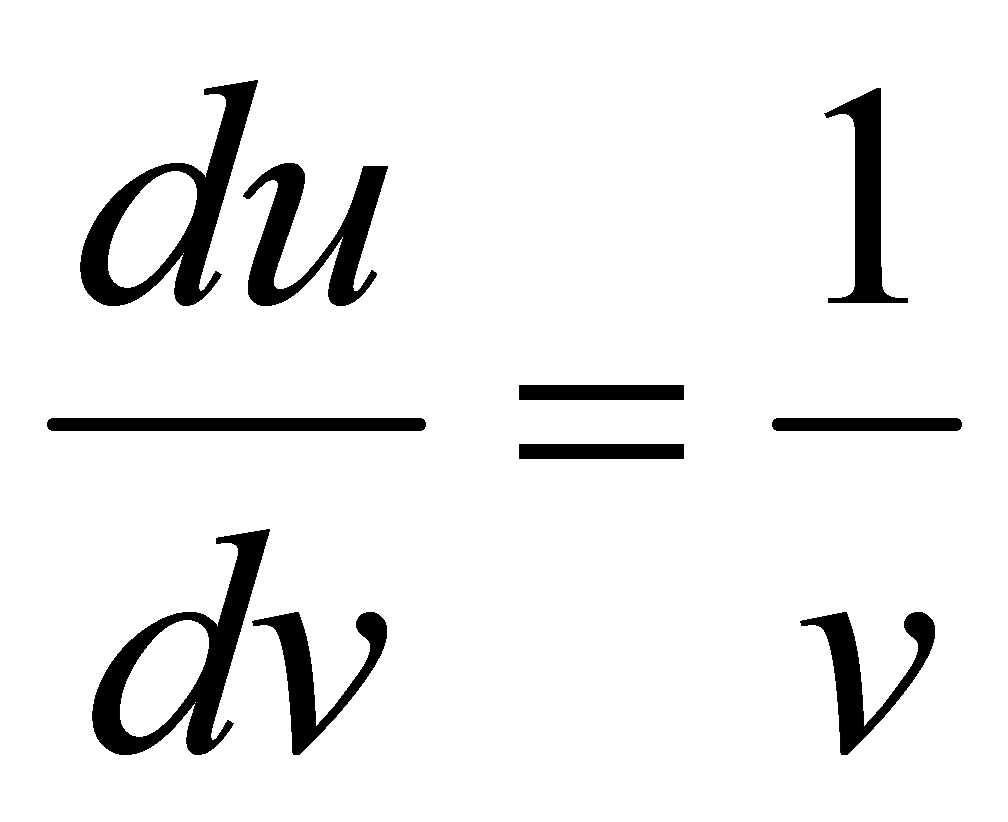 ,
,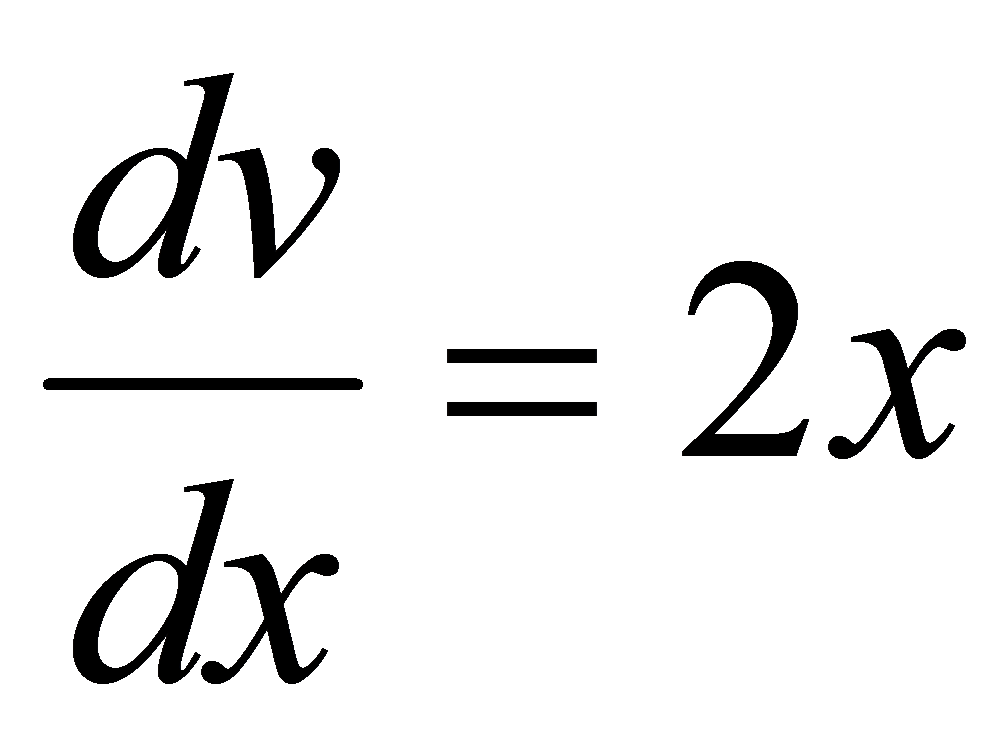 .
.
由(),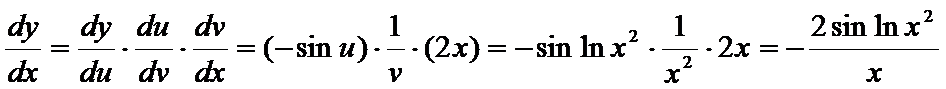 ,
,
即 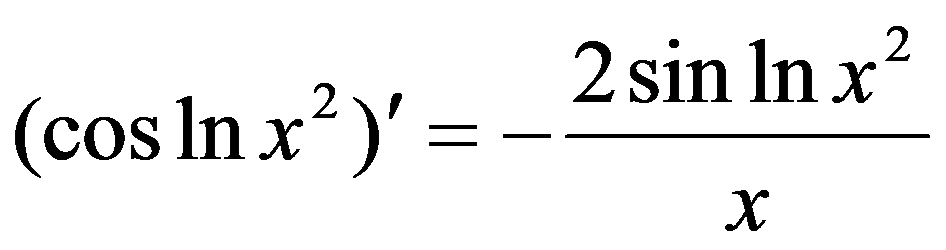 .
.
直接按照复合函数求导法则写出求导过程即是:
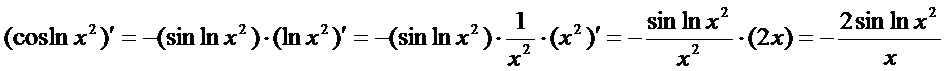 .
.
例求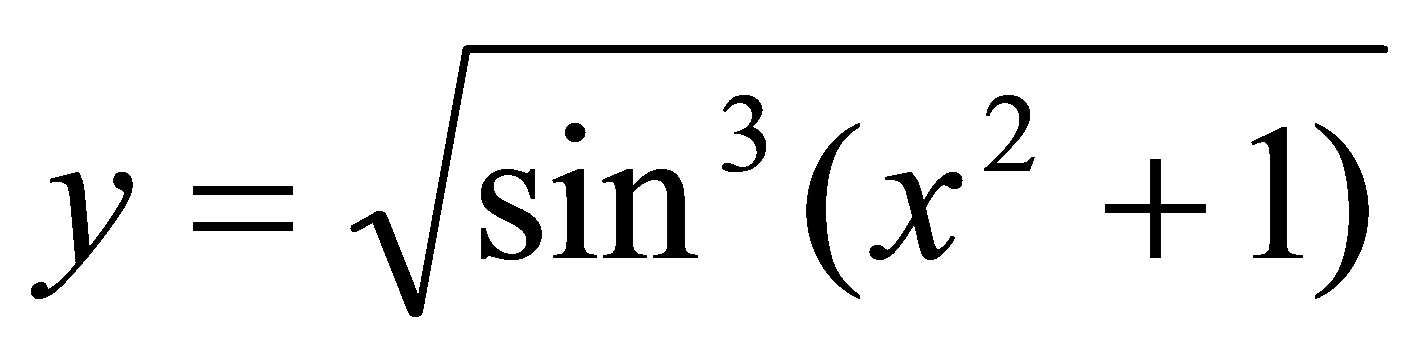 的导数.
的导数.
解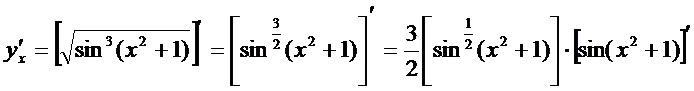
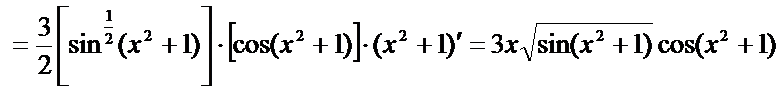 .
.
复合函数求导法的关键在于正确分析函数的复合结构. 复合函数求导法在求函数导数的运算中起着极为重要的作用,同时也是后面积分法中换元积分的基础. 因此是本门课程必须牢固掌握的基本功.
以下几类求导法,是复合函数求导法在特殊情况下的应用, 本质上都是复合函数求导法.